OMSCS への出願に際して、推奨されていた Georgia Tech が提供する MOOC の Data Structures & Algorithms を受講した。
Overall
ジョージア工科大学 OMSCS の出願準備のため、推奨される 3 つの MOOC の内 2 つを受講した。 Java に関する講座に関しては、以下にまとめている。
edX Introduction to Object-Oriented Programming with Java
Computer Science の基礎であり、ソフトウェアエンジニアの Tech Interview でもおなじみのデータ構造とアルゴリズムに関する授業であった。 講義で利用する言語は Java であり、データ構造やアルゴリズムの実装課題はすべて Java で書いて提出した。
Content
4 Part で構成されており、ボリュームとしては週 9-10 時間で 5 カ月ほど要するものである。 各 part は 3 つほどの Module に分かれており、データ構造やアルゴリズムに関して学んでいく形式であった。 小テスト、課題、確認テストで評価が決定し、60% 以上の成績で証明書が発行される。 以下のサイトは、本講座に出てくるデータ構造やアルゴリズムを可視化したものであり、動作のイメージをつかむのに有益だった。
CS 1332 Data Structures and Algorithms Visualization Tool
Data Structures
Part 3 の途中まではデータ構造に関する内容であり、それぞれのデータ構造に関しては、以下のように分類される。 各データ構造に関しては、上記の Visualization Tool を参考に概念図を示した。
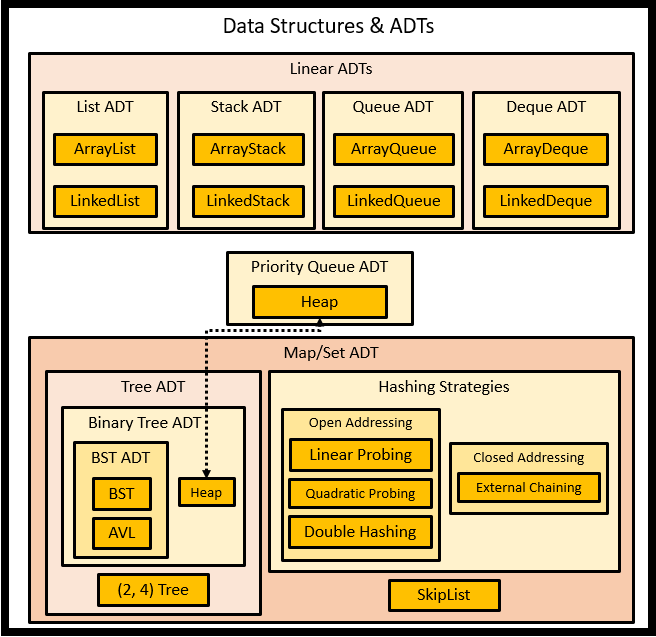
from edx Data Structures & Algorithms
Part 1 ArrayLists, LinkedLists, Stacks and Queues
Part 1 では、基本となる ArrayList, LinkedList, Stack, Queue について学習した。
- ArrayList
サイズが可変の配列で、要素が追加されると自動的にサイズが増える。 特定の要素にアクセスするスピードが早いが、要素を追加するスピードが遅い場合がある。 配列内の要素に対してランダムなアクセスが得意なデータ構造である。
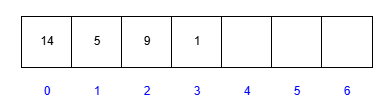
- LinkedList
各要素は次の要素を示す情報を持っている構成である。 データの末尾への追加が容易だが、順方向にのみ移動が可能である。

- Stack
スタックは、机の上に積まれた書類のようなデータ構造であり、一番最後に追加されたデータが最初に取り出される FILO(First-In, Last-Out) である。 Stack の実装には、array-backed と linked-backed に関して取り上げられていた。 以下の図は、Linked Stack である。
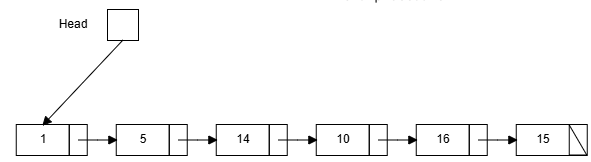
- Queue
行列の待機に近い構造で、最初に入ったデータが最初に取り出される FIFO (First-In, First-Out) である。 Queue に関しても、array-backed と linked-backed に関して触れられていた。 以下の図は、Linked Queue である。
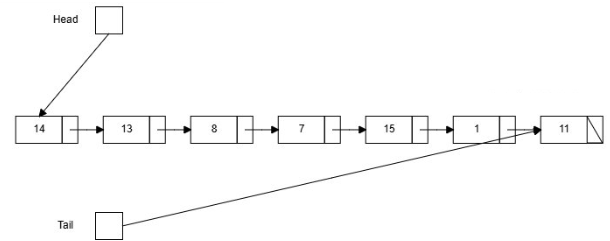
Part 2 Binary Trees, Heaps, SkipLists and HashMaps
Part 2 Binary Search Tree, Heap, SkipList, HashMap を取り扱った。
- Binary Search Tree
二分木は、ノードとエッジで構成されるデータ構造であり、各ノードは、最大二つの子のノードを持つ。
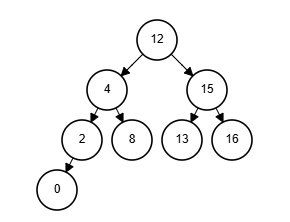
- Heap
データは優先度に基づいて整列され、親ノードの値が子ノードの値より小さい(Min heap)または大きい(Max heap)として実装される。 Priority Queue として使用される。 Array で実装することができ、親ノードは子ノードの index i の 1/2 となることから、i/2 に位置する。
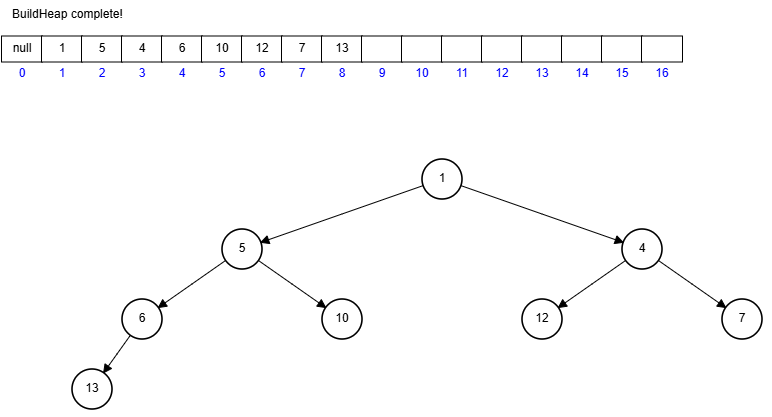
- SkipList
SkipList は LinkedList を高速に検索できるようにしたデータ構造であり、複数のレベルを持つノードで構成される。 高いレベルのノードは低いレベルのノードをいくつかスキップして実装するため、検索が早くなる場合がある。
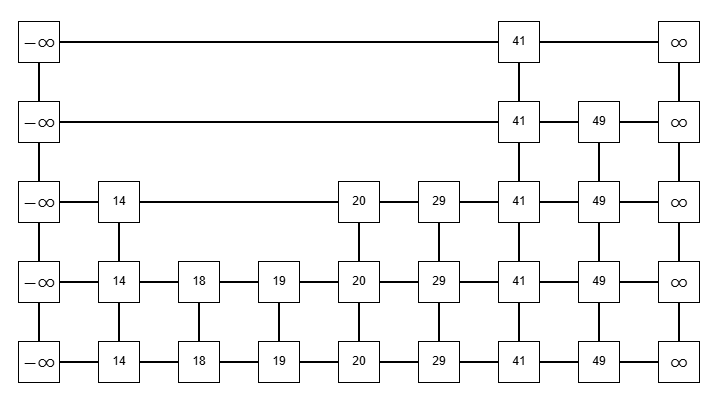
- HashMap
キーと値のペアを保持するデータ構造であり、キーをハッシュ関数でハッシュ値に変換し、配列のインデックスとして使用する。
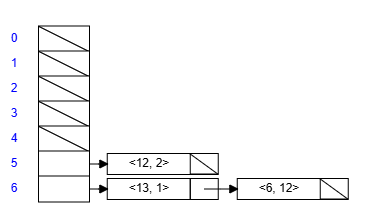
Part 3 AVL and 2-4 Trees, Divide and Conquer Algorithms
Part 3 では、データ構造としては AVL, 2-4 Tree に関して取り扱った。 Algorithm に関しても、Iterative Sorts, Divide & Conquer Sorts を取り扱った。
- AVL
Binary Search Tree (BST) で常にバランスとるような構造が AVL であり、どのノードの左右部分木の高さの差も1以下である。 BST では最悪の場合、一方にノードが偏ることで、探索が O(n) となるが、常にバランスすることで最悪ケースでも O(log (n)) となるようにしたもの。 ノードの追加・削除時に、この条件を満たさなくなると、Rotation という操作を行って左右部分木の高さを調節し、条件を満たすように木を変形する。
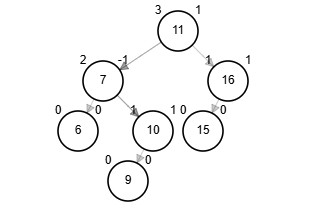
- 2-4 Tree
各ノードは2つから4つの子ノードを持ち、ノードの追加・削除時に、範囲条件を満たすようにノードを再配置する
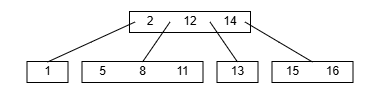
Algorithms
このコースで扱ったアルゴリズムの分類は以下の通りである。 アルゴリズムに関しては、各手法を概要を以下にまとめた。
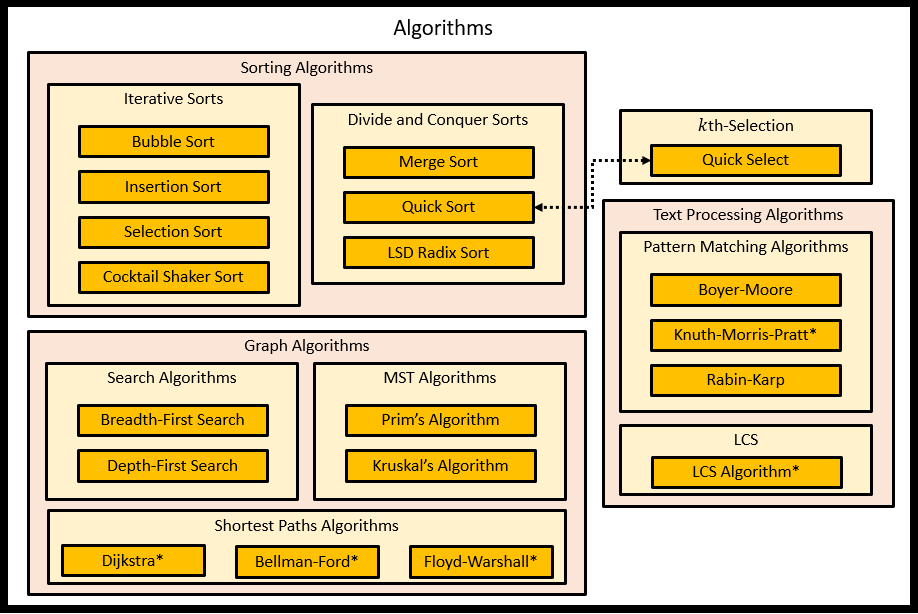
また、参考として共有されたそれぞれのソートを可視化した動画が以下になる。
15 Sorting Algorithms in 6 Minutes
Part 3 AVL and 2-4 Trees, Divide and Conquer Algorithms
Part 3 に関しては、Iterative Sorts, Divide & Conquer Sorts を取り扱った。 Iterative Sorts は、Bubble Sort に代表されるような、繰り返しによってソートする Algorithm である。 Divide & Conquer Sorts に関しては、大きな問題を複数の小さな問題に分割し、それぞれを個別に解いてから統合する手法である。
Iterative Sorts
- Bubble Sort : 隣接する要素を比較して、必要に応じて交換することで並び替える手法
- Insertion Sort : 未整列部分の要素を適切な位置に挿入して整列させる手法
- Selection Sort :未整列部分から最小の要素を選んで整列させる手法
- Cocktail Shaker Sort : バブルソートの改良版で、交互に左右にスキャンしながら、隣接する要素を比較して交換する手法
Divide & Conquer Sorts
- Merge Sort : 大きな数列を小さな数列に分割し、それぞれを並べ替えた後、再び統合して最終的にソートされた数列を算出する方法。
- Quick Sort : ピボット値を選択し、その値を中心に数列を分割してソートを行う手法。
Part 4 Pattern Matching, Dijkstra’s, MST, and Dynamic Programming Algorithms
Part 4 では、テキストにおける Pattern Matching, Graph Algorithms, Minimum Spanning Trees (MST), Dynamic Programming に関して学んだ。
Pattern Matching
- Boyer-Moore (BM) : 探索文字列を後方から比較する点が特徴であり、テキストと探索文字列の最後の文字を比較し、不一致があった場合は、探索文字列の2番目の文字の位置を記憶して探索を進める。
- Knuth-Morris-Pratt (KMP) : テキストと探索文字列を先頭から1文字ずつ比較するが、文章の中に探索文字列の先頭から合致する位置を記憶することで、一致しない場合に探索する探索文字列をスキップするのが特徴的である。
- Rabin-Karp (RK) : ハッシュ関数を使用して探索文字列とテキストの一部のハッシュ値を計算し、値が一致する場合に実際に文字列の比較を行う。
Graph Algorithms
- Breadth-First Search : Start Vertex から隣接する Vertex を優先して探索する方法で、次に訪れる Vertex を Queue で管理する。
- Depth-First Search : Start Vertex から離れる Vertex を優先して探索する方法で、次に訪れる Vertex を Stack で管理する。
- Dijkstra’s : グラフ理論における辺の重みが非負数の場合の単一始点最短経路問題を解く方法であり、Priority Queue を用いて、最小の重みの Vertex を選択する。
Minimum Spanning Trees (MST)
- Prim’s Algorithm : Edge の重みの総和が最小となる Minimum Spanning Tree (MST) を探索する手法であり、一つの Vertex から開始し、Priority Queue を用いて最も重みの低い Edge を選択していく。密なグラフに適している。
- Kruskal’s Algorithm : MST を探索する手法であるが、全ての Edge から重み低い順に Edge を確認し、追加していく手法である。疎なグラフに適している。
Dynamic Programming
- Longest Common Subsequence (LCS) : 与えられた二つの文字列の最長共通部分列 (LCS) を求める手法で、テーブルを構築し、文字列の比較を行う。
- Bellman-Ford : 単一の出発点からすべての頂点への最短経路を求める手法で、負のエッジの重みを持つグラフでも動作する。グラフ内のエッジを反復的に緩和することで、すべての頂点への最短経路を見つける。
- Floyd-Warshall : すべての vertex 間の最短経路を求める手法で、すべての Vertex のペアに対して最短経路を計算する。
Reflection
多くのデータ構造、アルゴリズムを学ぶことができたコースであったが、ツールが非常に優秀で動作をイメージしやすく理解の助けになった。 一部に関しては課題を通して実装したため、理解を深めることができた。実際に LeetCode を解いてみると、この講義で学んだことを利用するような問題もあった。 今回は講義の中で実装のヒントなどもあり実装することができたが、今後はこれらを自在に操れるようになっていきたいと思う。